AUTHORS: Zhiyong Zhu, Enmei Dong

Download as PDF

ABSTRACT:

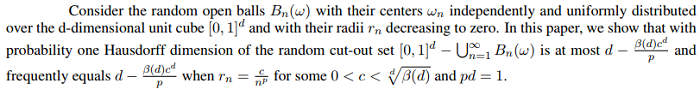
KEYWORDS: Fractal, Random fractal, Random measure, Random cut-out set

REFERENCES:

[1] M. F. Barnsley, Fractal everywhere, Academic Press, New York, 1988.

[2] B. B. Mandelbrot, The fractal geometry of nature, Freeman, San Francisco, 1982.

[3] B. B. Mandelbrot, Renewal sets and random cutouts, Z. Wahrscheinlichkeitstheorie verw Gebiete. 22, 1972, pp. 145-157.

[4] U. Zahle, Random fractals generated by random cutouts, Math. Nachr. 116, 1984, pp. 27-52.

[5] B. B. Mandelbrot, The fractal geometry of nature, San Francisco 1983.

[6] K. J. Falconer, Random fractals, Math. Proc. Camb. Phil. Soc.100, 1986, pp. 559-582.

[7] S. Graf, R. D. Mauldin and S. C. Williams, The exact Hausdorff dimension in random recursive constructions, Mem. Am. Math. Soc.71(381), 1988, pp. 1-121.

[8] R. D. Mauldin, S. C. Williams, Random recursive constructions: asymptotic geometric and topological properties, Trans. Am. Math. Soc. 295, 1986, pp. 325-346.

[9] N. Serban, W. Wendelin, Random soups, carpets and fractal dimension, Journal of the London Mathematical Society. DOI: 10.1112/jlms/jdq094.

[10] K. J. Falconer, Techniques in fractal geometry, Chichester: John Wiley and Sons, 1997.

[11] K. J. Falconer, Fractal Geometry: Mathematical Foundations and Applications, 2nd Edition, West Sussex: John Wiley and Sons, 2003.

[12] D. Gatzouras, S. P. Lalley, Statistically selfaffine sets:Hausdorff and box dimensions, J. of Th. Probab.7, 1994, pp. 437-468.

[13] S. Graf, Statistically self-similar fractals, Prob. Th. Rel. Fields.74, 1987, pp. 352-392.

[14] A. S. Besicovitch, S. J. Taylor, On the complementary intervals of linear closed sets of zero Lebesgue measure, J. London Math. Soc.29, 1954, pp. 449-459.

[15] B.B. Mandelbrot, On Dvoretzky coverings for the circle, Z. Wahrscheinlichkeitstheorie verw. Geb. 22, 1972, pp. 158-160.

[16] A. Dvoretzky, On covering a circle by randomly placed arcs, Proc. Nat. Acad. Sci.42, 1956, pp. 199C203.

[17] L. Shepp, Covering the circle with random arc, Israel J. Math. 11, 1972, pp. 328C345.

[18] L. Shepp, Covering the line with random intervals, Z. Wahrsch. Verw. Gebiete23, 1972, pp. 163C170.

[19] J. P. Kahane, Some random series of functions, Cambridge University Press, 1985.

[20] J. Barral, A. H. Fan, Covering numbers of different points in Dvoretzky covering, Bull. Sci. Math. 129, 2005, pp. 275C317.

[21] A. H. Fan, How many intervals cover a point in the Dvoretzky covering? Israel J. Math. 131, 2002, pp. 157C184.

[22] A. H. Fan, J. Wu, On the covering by small random intervals, Ann. Inst. H. Poincare Probab. Statist. 40, 2004, pp. 125C131.

[23] E. Ja¨rvenpa¨a¨, M. Ja¨rvenpa¨a¨, H. Koivusalo, B. Li, and V. Suomala, Hausdorff dimension of affine random covering sets in torus, Ann. Inst. H. Poincar Probab. Statist. 50, Number 4 ,2014, pp. 1371-1384.

[24] Robert B. Ash, and Catherine A. DoleansDade, Probability and Measure Theory, Academic Press, San Diego, 2000.

[25] M. Muresan, A Concrete Approach to Classical Analysis, Springer 2008.