
Plenary Lecture
Problem of Minimum Mass for a Particular Tensegrity Structure

Assistant Professor Rosario Montuori
Department of Civil Engineering
University of Salerno
ITALY
E-mail: r.montuori@unisa.it
Abstract: Tensegrity systems represent one of the more recent structural typologies in the field of civil en-gineering; in fact, Tensegrity systems have been introduced in 1950s. In this work a particular Tensegrity system is considered, the so called T-Bar depicted in figure 1. It is well known that a tensegrity structure is composed by bars and cables, with bars typically loaded in compression, and cables in tension.
In this work the author provides relations to design tensegrity structures for minimal mass when both local and global buckling are considered.
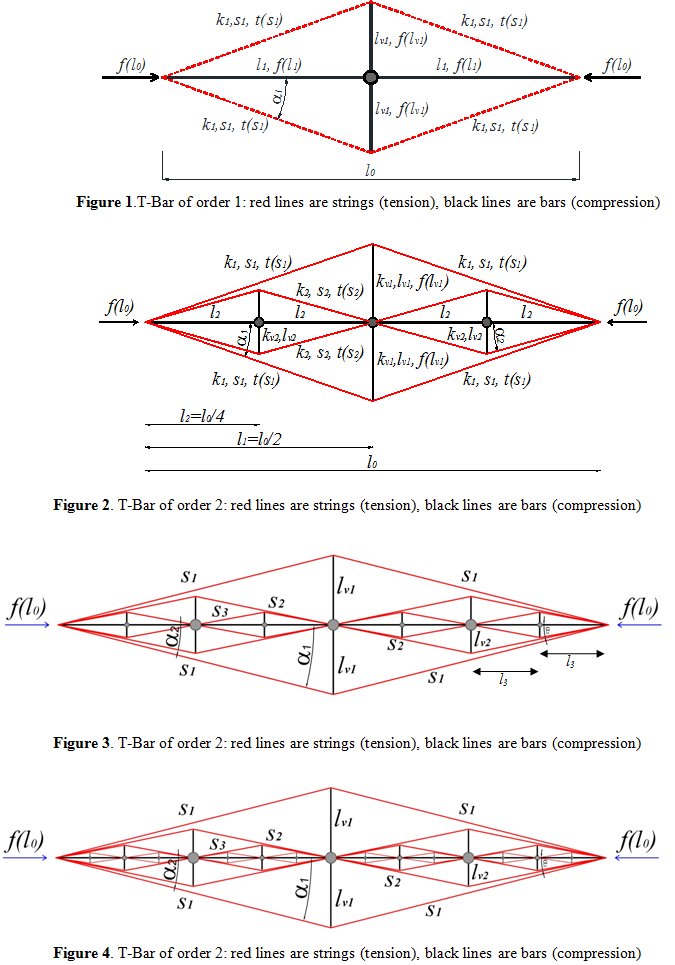
The originality of the work is due to the consideration of global instability that was not accounted for in the previous studies. In fact, the result already found by R. E. Skelton and M. C. de Oliveira. (Tensegrity Systems. Springer, 2009.) minimized mass subject to only local buckling. In order to prevent also global buckling, the author show that the total mass found in this study is always greater or equal to the one found in the previous study. The result shows explicitly the conditions under which the original design (Skelton and de Olivera) holds and when it does not, and the formula for the minimal mass is given when global buckling limits the mass, instead of local buckling. In addition, the mathematical formulation is presented for T-bar of order greater than 1. In fact, a T-Bar of order 2 can be obtained from the T-Bar reported in Figure 1 by substituting the two bars of length l1 with two T-bars, as depicted in figure 2. The obtained structure is defined as a T-Bar of order two. Similarly, by substituting the four bars having length l2 with four T-Bars, the T-Bar of order 3 depicted in figure 3 is obtained, and by substituting the eight bars of length l3 with eight T-Bars, the T-Bar of order 4 depicted in figure 4 is determined.
The work shows how to write the matrix for the solution of the general problem which is provides a matrix of order 2n where n is the order of the considered T-bar. The obtained matrix has been solved in some particular cases by means of Wolframe Mathematica 8 computer program.
Brief Biography of the Speaker: Rosario Montuori is an Aggregate Professor in Structural Engineering in the Department of Civil Engineering of the University of Salerno, Italy since 2005. He received the M.S/B.S. in Civil Engineering from the University of Salerno (ITALY) in 1997 and the PhD in Structural Engineering from the same University in 2001. He is author of more than 100 journal articles, conference papers and scientific reports. His principal research activities are devoted to the control of collapse mechanism for steel structures by means of a rigorously application of “capacity design”. In particular, the research activities concern the following structural typologies: Moment Resisting Frames with semi-rigid joints, Irregular Moment Resisting Frames, Concentrically “X” and “V” Braced Frames, Concentrically “X” Braced Frames with Reduced Section (reduction of the cross section area at the ends of the bracing members), Eccentrically Braced Frames, Moment Resisting Frame-Concentrically Braced Frame dual systems and Truss Moment Frames with special devices located at the bottom chord level at the ends of the truss girders.
For several of the considered structural typologies, also the seismic structural reliability defined as the mean annual frequency (MAF) of exceeding a threshold level of damage, i.e. a limit state has been investigated and compared with reference both to the proposed design methodologies and to EC8 provisions.
He developed a theoretical fiber models able to predict the Moment-curvature behaviour of RC columns strengthened by means of angles and battens. He developed also a theoretical fiber models able to predict the Moment-curvature behaviour of Concrete Filled steel Tubular columns (CFT) with Square Hollow Section (SHS). Both the proposed models have been validated by means of experimental tests.
In the field of innovative Tensegrity structures he is developing models that can take into account the phenomenon of global instability, which can play a fundamental role when the design is devoted to the minimum mass solution.
He has participated as research staff member in various research projects funded by the Italian Ministry of Education and the Italian Network of Seismic Engineering Laboratories (ReLUIS).
He serves as a reviewer for several international journals.